Research

Gated Reactions

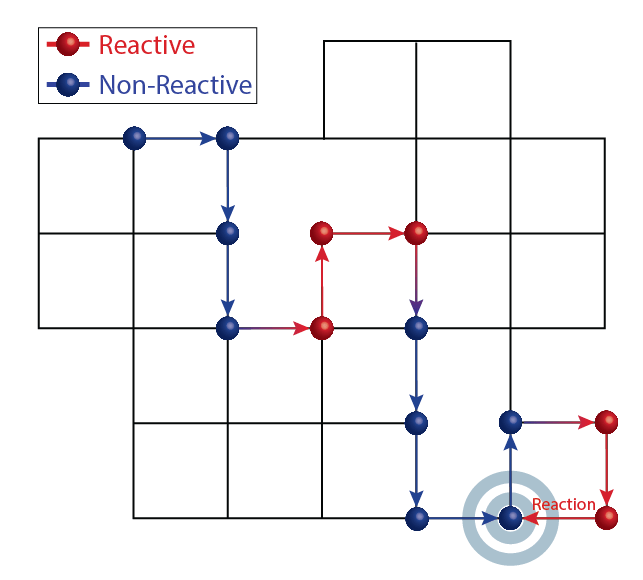
Gated Reactions are reactions in which the reactants switch stochastically between reactive and non-reactive states, and reaction can only occur if two reactants meet while being in the reactive state.

We have written a trilogy of papers in which we have developed general formalisms to treat gated reactions. In these papers, we derived relations between ungated reaction times and their gated counterparts and used them to distill universal features of gated reactions. We have done so, respectively, for networks (continuous-time random walks), discrete time and space and continuous time and space. The relations we have found greatly simplify the analysis of gated reactions compared to direct, brute-force, approaches. Indeed, we demonstrated how one can use them to provide a clean and simple derivation of classic results as well as solutions to problems that were previously considered intractable. Different examples are employed in each paper, ranging from a continuous-time random walk on an arbitrary network, unidirectional motion on a ring, to a drift-diffusion process. In each paper we inevitably deal with unique phenomena that emerge due to the topological properties of time and space. For example, the discretization of time gives rise to a phenomena that do not exist in the continuous-time analogue (apart from the deterministic limit). Crucially, when the internal gating dynamics is in (out of) phase with the spatial process governing molecular encounters resonance (anti-resonance). Another example is the explicit introduction of volume in continuous space, and hence the possibility of dealing with finite-sized targets, or even an infinite target which naturally arises in the problem of threshold crossing.

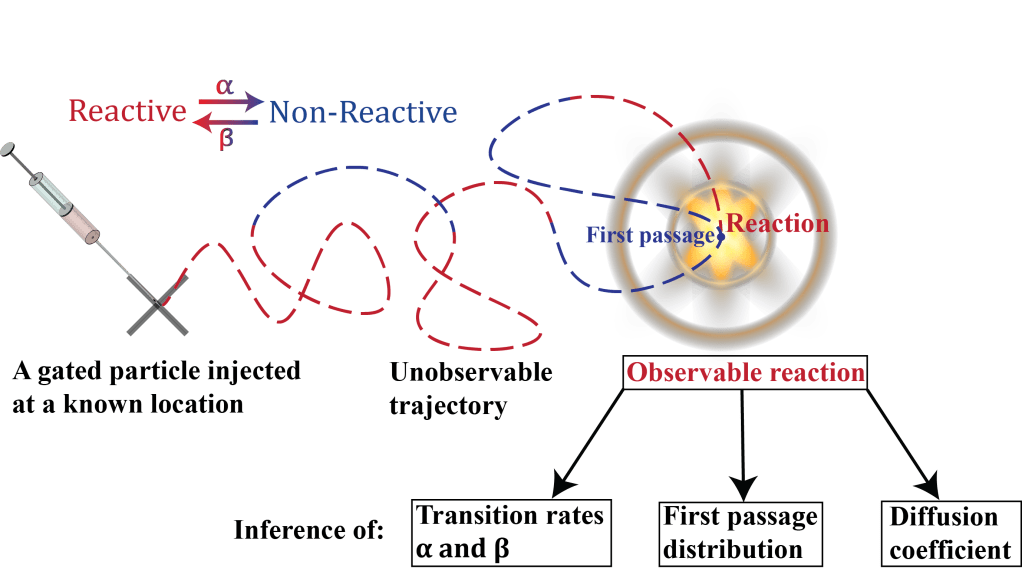
Inference from Gated First-Passage Times

The first-passage time is a quantity of considerable interest in many areas. However, in realistic scenarios, various forms of “gating” prevent first-passage times from being directly accessible. The crucial challenge is then to infer the first-passage time statistics from gated observations, i.e., from the actual times at which events are detected. In our paper, Inference from Gated First-Passage Times, we provide a universal, model free, scheme which solves this long-standing inference challenge.

Gated first-passage processes cover a broad spectrum as they occur in chemical reactions, time series analysis, and sensor detection problems. They are also especially relevant to the emerging fields of single-molecule and nano-scale chemistry, which gather immense interdisciplinary research interest. In these and other real-life examples, inferring fundamental properties of an underlying first-passage process of interest from gated detection times is a key challenge.

Motivated by this inference challenge, and the complete lack of results on this front, we developed a theoretical framework for inference in gated first-passage processes. We derived relations between the statistics of detection times and a series of hidden quantities that one might wish to infer [Equations 3, 6, 7, 8 and 9]. These relations were corroborated, both analytically and numerically, on two classical models with a strong experimental appeal: the birth-death process, and diffusive target search. Remarkably, the universality of our results allows for the inference of the unknown first-passage statistics without needing to know or assume the underlying laws of stochastic motion. Furthermore, by exploiting the above relations, we obtain novel fundamental relations between the detection time, first-passage time, and the propagator of the underlying process [Equations 4 and 5].

Being first of its kind, our approach opens new avenues connecting experimental and theoretical research, e.g., by allowing the inference of diffusion coefficients and gating rates in situations where these are concealed from direct observation.

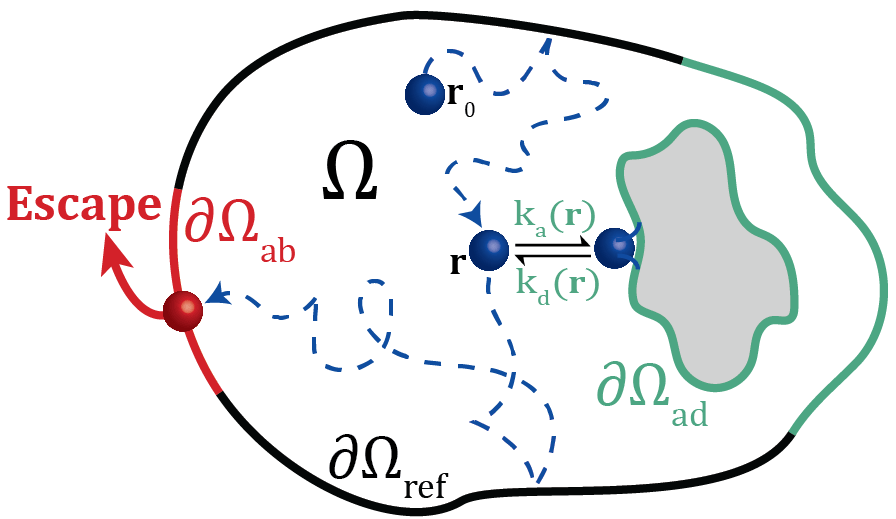
Escape of a Sticky Particle

A myriad of systems, ranging from biological organelles to man-made nanodevices, exhibit “stickiness”. We use stickiness as a broad encompassing term, since the list of possible physical origins covers surface adsorption (chemical and physical adsorption), reversible binding, trapping, and more. We modeled a sticky boundary with the adsorption-desorption framework, and point out that exact solutions for the escape times of particles diffusing in domains of mixed boundaries – sticky, absorbing, and other types – are unknown to date. In our paper, Escape of a Sticky Particle, we presented a general approach to mathematically pose and analytically solve this problem.

A paramount setting that is central to our analysis is a domain with a mixture of sticky and absorbing boundaries. A question that is then often asked is “How much time does it take a diffusing particle to escape, i.e., reach the absorbing boundary, in such a domain?”. Cleary, stickiness can have a dramatic effect on the escape time. Yet, despite the prevalence of such scenarios, exact solutions are unknown; and previous attempts that highlighted the need to include stickiness in biophysical settings only did so by using approximations, thus testifying to the significant challenges posed by the task at hand.

In our work, we provided the first derivation of the partial differential equations governing the escape time of a diffusing particle from a domain of arbitrary dimension, geometry, and surface reactivity. The effect of stickiness is thoroughly analyzed and explained via the paradigmatic example of a slab domain for which we explicitly calculated the escape time distribution, mean and variance, and distilled generic insights. We further leveraged this case study to construct a scheme for inference of the adsorption-desorption rates from experimental data, and to propose an accurate way of simulating diffusive dynamics in arbitrary sticky domains.

The theory developed also applies more broadly in the context of first-passage problems in sticky environments. Moreover, our approach opens new avenues connecting experimental and theoretical research, e.g., by allowing the inference of adsorption-desorption rates. This is a challenging experimental problem, especially for biochemical reactions in living cells, for which such rates are often unknown or known only with a very poor accuracy. We thus believe our work will attract broad attention from both theoreticians and experiments and will stimulate future efforts on the effect of stickiness and morphological features.

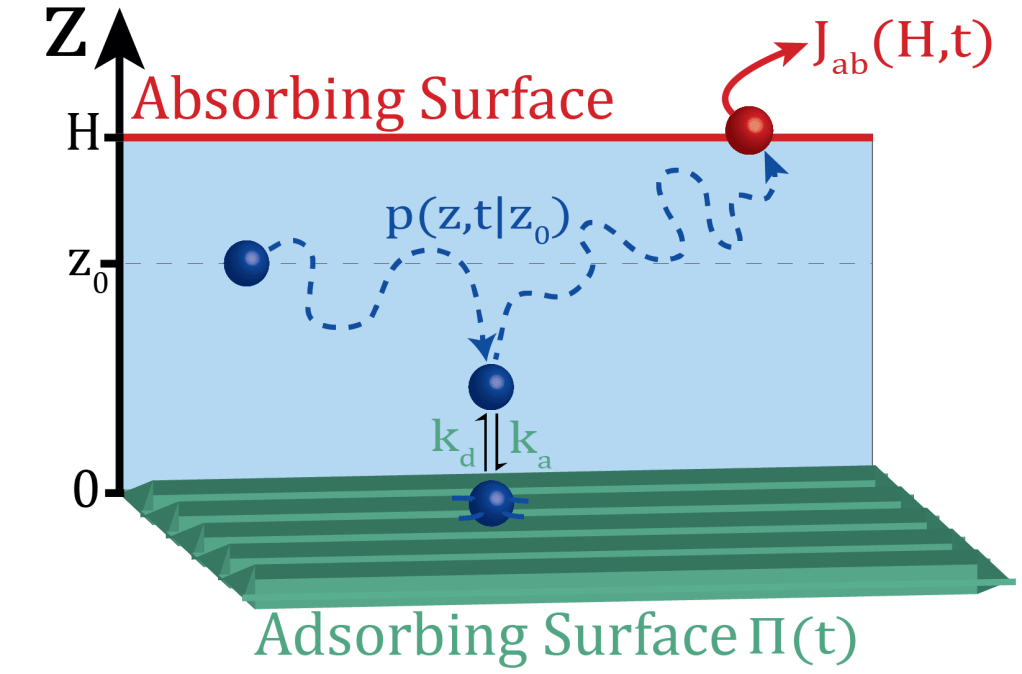
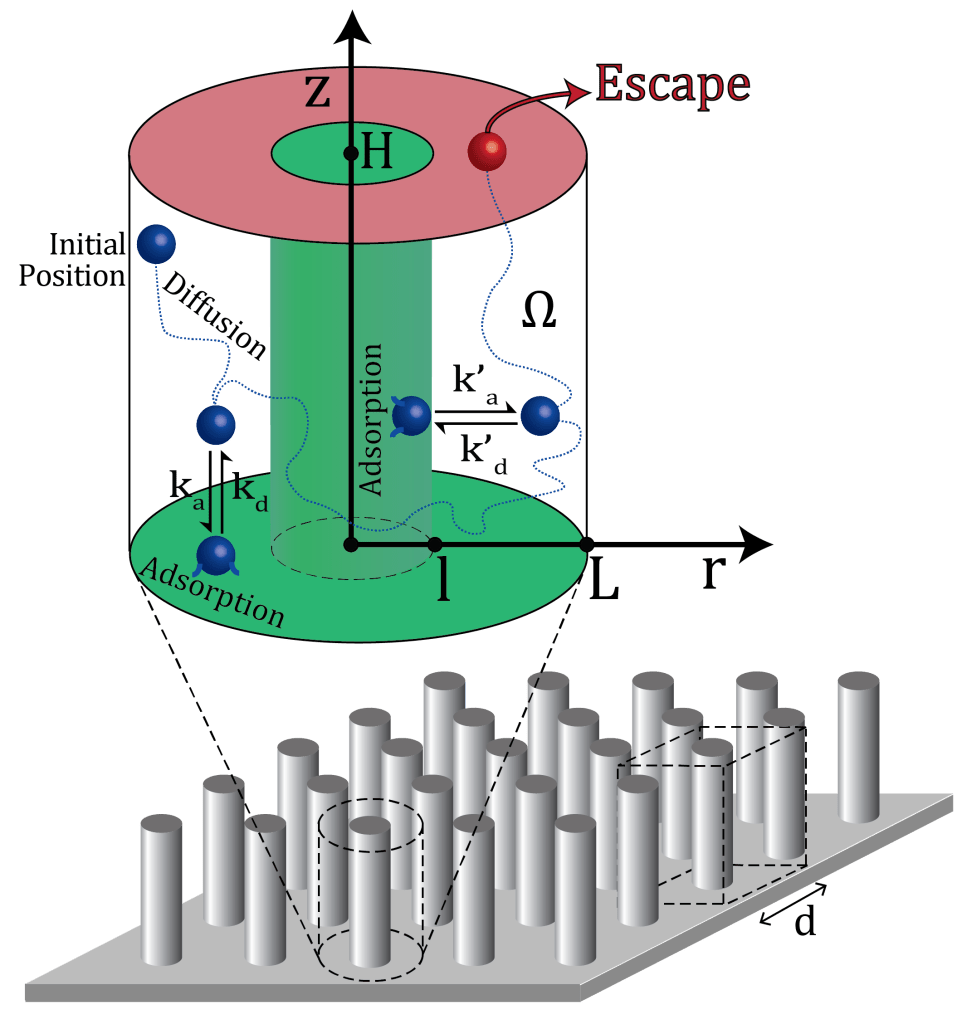
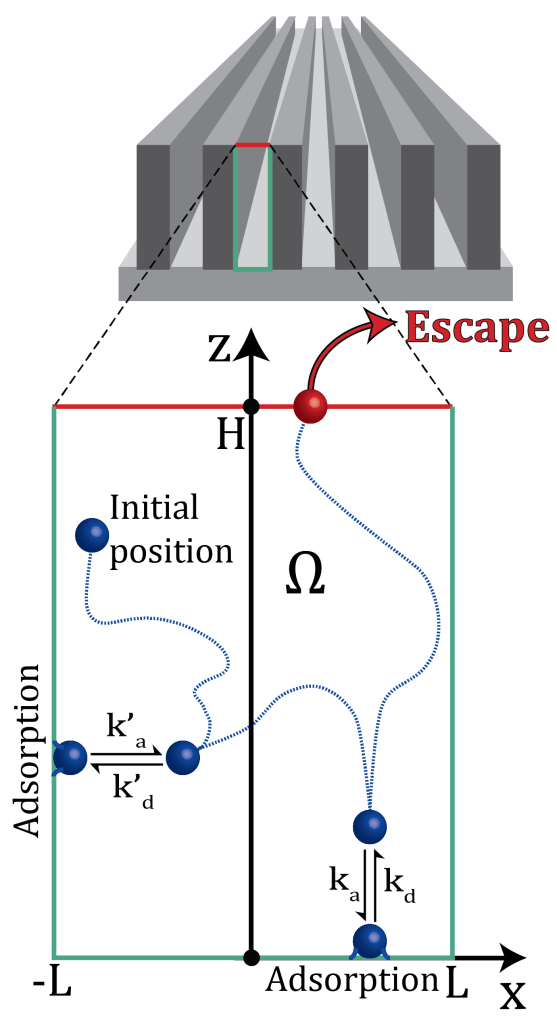
Escape from Textured Adsorbing Surfaces

In Escape from Textured Adsorbing Surfaces, we investigated the desorption properties of three prevalent nanostructures (holes, pillars, and grooves) through the analysis of the escape time from the confining spaces within these textured surfaces. In doing so, we are in fact the first to solve analytically for the diffusive escape time out of adsorbing textured surfaces (so far only smooth surfaces were considered, flat or curved). Our analysis also yielded scaling laws which elucidate how surface topography affects the desorption rate from a textured surface. As these scaling laws seem to be universal, they will surely find use in a host of scientific and technological domains.

The cutting-edge experiments from the group of Fernando Patolsky in Tel-Aviv University inspired us to solve the problem of escape from a textured adsorbing surface analytically. In the experiments, an intriguing effect of the topographical properties of adsorbing surfaces was observed: vertical arrays of antibody-modified Si nanopillars were able to capture biomolecules for extremely long times (weeks and even months). The same antibody, if used on a flat surface, would bind the biomolecules for a few milliseconds only. Similarly, using the nanopillar vertical array without antibodies leads to a fast diffusive escape. The dramatic effect of prolonged escape times is hence a result of a combination of topography and stickiness (adsorption).

To better understand the interplay between surface topology and desorption, we derived the probability density function and the mean escape time from textured surfaces and corroborated the results with Monte-Carlo simulations. The escape time (and hence the effective desorption rate) was shown to abide a universal scaling law, which couples the equilibrium constants of adsorption with the relevant confining length scales. The generality of our results suggests that they can be used, as first approximations, to explain desorption from more complicated topographies which were not considered in our analysis.

During the last two decades there has been a rapid advance in fabrication of nanoscale topographies. As presented in the introduction to our paper, the joint effect of topography and stickiness can also be cardinal when considering catalytic surfaces, or living cell behavior (protein adsorption to a textured surface mediates the cell attachment to the surface).

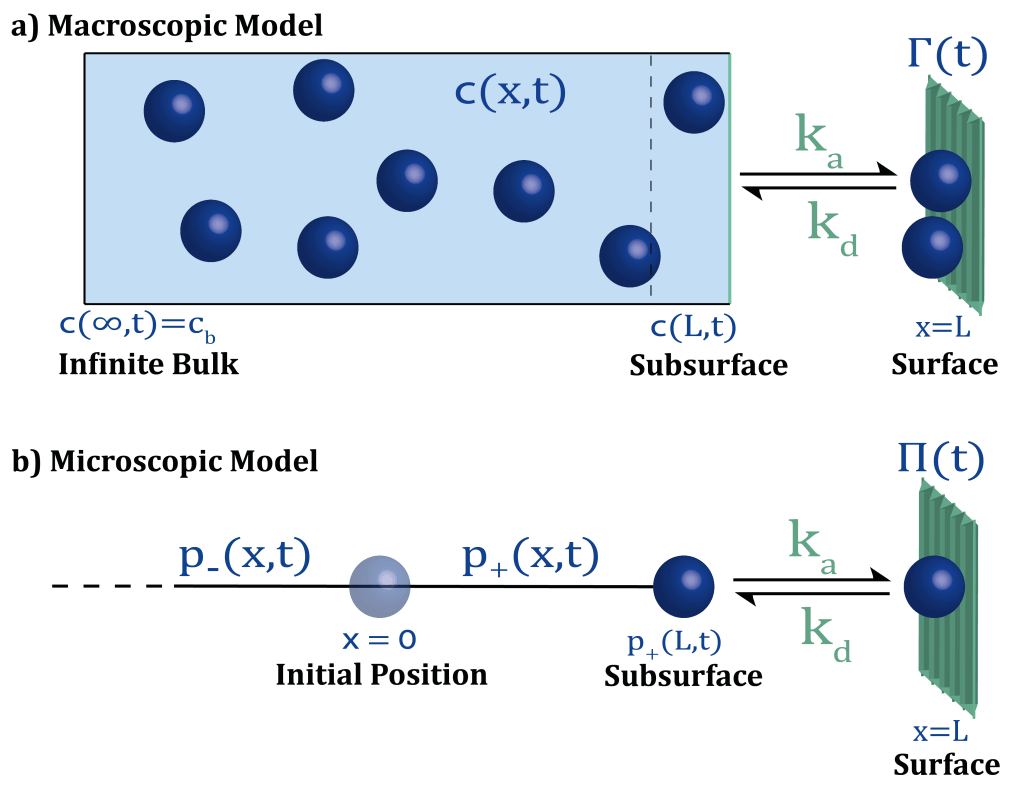
Theory of Single-Particle Adsorption Kinetics

In Theory of Single-Particle Adsorption Kinetics, we provided a self-contained and detailed theory of single-particle adsorption kinetics, which extends the existing macroscopic theory and relate to it. We exemplified the general theory by investigating two fundamental models, diffusion in an adsorbing one-dimensional tube and diffusion inside an adsorbing spherical shell.

Since the seminal work by A.F.H. Ward and L. Tordai in The Journal of Chemical Physics in 1946, the field of dynamic surface adsorption kinetics has seen many contributions, which we briefly reviewed in Sec. II of our work. Ward and Tordai are credited for postulating the relation between the surface concentration and the sub-surface concentration in their model of one-dimensional infinite bulk of adsorbates, and unspecified surface dynamics. In our work, we generalized this result to arbitrary dimension, geometry, and initial conditions (specifically, we also consider the single-particle analog). We believe that a proper interpretation of the Ward-Tordai relation was so far missing from the literature. To this end, we also provided a thorough and modern interpretation of the renowned Ward-Tordai model.

We believe that the equations accounting for the models investigated in our work can be of use to experimentalists, whether in the characterization of adsorption and desorption rates or in experiments design.

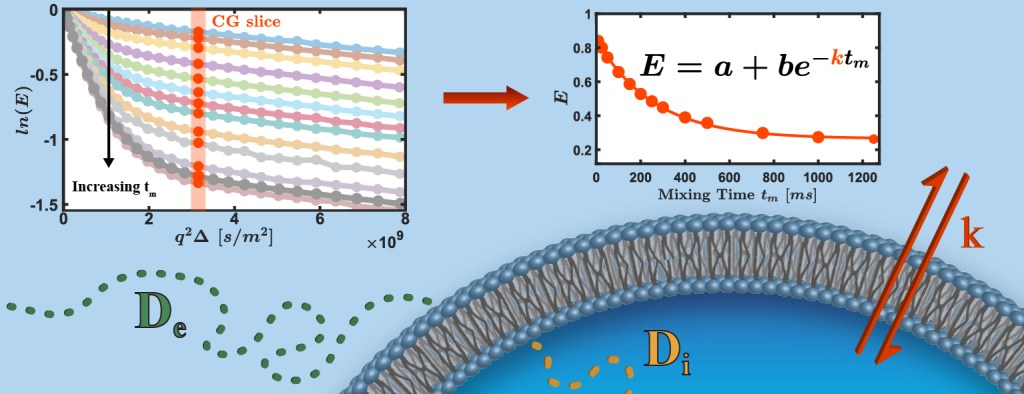
Diffusion-MR: Measurement of Transmembranal Exchange Rate

Determining the structural characteristic and dynamics of micro-scale porous systems is of great interest in many fields, as they impose physical properties and functionalities. Diffusion magnetic resonance techniques, which encompass both spectroscopy and imaging, were shown to allow for such determination completely non-invasively, thus being applicable, inter alia, to in vivo study of biological tissues, and particularly to the study of neuronal tissues, which exhibit distinct structural characteristics (of great interest in that regard are axons, the long projections of neurons that comprise the white matter found in our brains.). An obvious implication of that, is the importance of diffusion magnetic resonance in characterization of normal tissues, diagnosis of pathological tissues, and in pathophysiological research.

We have focused on methods for measurement of the transmembranal exchange rate in biological systems (e.g., in yeast samples and porcine optic nerves). In a JMR communication we introduced a considerable shortening of the experiment time of a certain popular method called FEXSY, without jeopardizing the accuracy of the measurement. Our contribution is expected to have important practical implications once exchange-based methods are used in human clinical scanners, where the available time is limited and expensive.